5. Teaching Mathematical Reasoning: Critical Math Thinking Through Problem-Solving and Modeling
What is mathematical reasoning? The short answer is that is that is reasoning with math, and in a sense, it’s the skill that underlies all other math skills.
Math reasoning is not just skill in completing math worksheets or the math section on a standardized test. It involves skill in integrating math knowledge into real-life and everyday problems and using math to conceptualize complex problems that aren’t inherently mathematical themselves.
Developing skills in mathematical reasoning can contribute significantly to students’ overall critical thinking skills. It’s also central to being proficient in math and being able to solve math problems.
In this article, we outline two approaches to fostering mathematical reasoning skills and improved critical thinking in math:
- Mathematical problem-solving: This approach makes students think conceptually about problems before applying tools they’ve learned.
- Mathematical modeling: Modeling projects give students experience in weighing several factors against one another and using mathematical knowledge to make decisions.
I. Mathematical Problem-Solving
An emphasis on open-ended mathematical problem-solving can help develop mathematical reasoning skills and address a problem teachers have long been concerned about: too much “rote” learning in math.
Too often students spend time in math class memorizing procedures and applying them mindlessly to problems. This leads to errors when students are confronted with unfamiliar problems. It also contributes to a widespread misperception of math as boring and lacking relevance to everyday life.
On the other hand, attempting to remedy this problem by giving students open-ended problems has its own drawbacks. Without the conceptual and methodological tools to solve these problems students become frustrated and disengaged. It can end up being an inefficient way to spend class time.
Although learning fundamental math skills like algorithms for adding, subtracting, multiplying, and dividing is absolutely critical for students in the early grades, the deeper mathematical problem-solving skills are the ones we really want students to graduate with. How can we ensure they do?
- Create beneficial habits of mind — persistence, thoroughness, creativity in solution-finding, and improved self-monitoring.
- Break down hard problems into easier parts or reframing problems so that they can think about them more clearly.
- Some problem solving tactics are applicable to situations well beyond math: making a visualization of a situation to understand it more clearly; creating a simplified version of the problem to more easily address the essence of the problem; creating branches of possibilities to solve the problem; creating “what if” example cases to test key assumptions, etc.
- Elevate the value of discussion and argumentation over simple appeals to authority.
This process continues until the class has thoroughly explored the problem space, revealing multiple solution paths and exploring variations on the problem or contrasting problem-types.
Of course, the usefulness of a question like this depends on what students already know. If students don’t already know that chickens have two legs and pigs have four, they’re just going to be confused by the problem (and the explanation of the solution). It also requires some other basic skills—for instance, that if one chicken has two legs, four chickens would have eight.
As a way of evaluating student growth, teachers could also include some of these open-ended problems in homework assignments or as extra credit assignments.
Lesson Plan Outline
An example that might be appropriate for fifth grade is something like the following:
A farmer has some pigs and some chickens. He finds that together they have 70 heads and 200 legs. How many pigs and how many chickens does he have?
Divide the class into student groups of three to four. Have students spend a few minutes reading over the problem individually. Then let student groups discuss possible solution paths. The teacher walks around the classroom, monitoring the groups. Then the teacher leads a whole-class discussion about the problem.
- So how did you go about thinking about the problem?
- Show us how you got your answer and why you think it’s right. This might mean that a student goes up to the board to illustrate something if a verbal explanation is inadequate.
- And what was the answer you got?
- Does anyone else have a different way of thinking about the problem? If there are other ways of solving the problem that students didn’t come up with, teachers can introduce these other ways themselves.
Developing Math Problem-Solving Skills
Teachers should keep in mind the following as they bring mathematical problem-solving activities into their classrooms:
- Problem selection. Teachers have to select grade-appropriate problems. A question like “John is taller than Mary. Mary is taller than Peter. Who is the shortest of the three children?” may be considered an exercise to older students — that is, a question where the solutions steps are already known — but a genuine problem to younger students. It’s also helpful when problems can be extended in various ways. Adding variation and complexity to a problem lets students explore a class of related problems in greater depth.
- Managing student expectations. Introducing open-ended math problems to students who haven’t experienced them before can also be confusing for the students. Students who are used to applying algorithms to problems can be confused about what teachers expect them to do with open-ended problems, because no algorithm is available.
- Asking why. Asking students to explain the rationale behind their answer is critical to improving their thinking. Teachers need to make clear that these rationales or justifications are even more important than the answer itself. These justifications give us confidence that an answer is right. That is, if the student can’t justify her answer, it almost doesn’t matter if it’s correct, because there’s no way of verifying it.
II. Mathematical Modeling
Another approach is mathematical modeling. Usually used for students in middle or high school, mathematical modeling brings math tools to bear on real-world problems, keeping students engaged and helping them to develop deeper mathematical reasoning and critical thinking skills.
Math modeling is an extremely common practice in the professional world. Investors model returns and the effects of various events on the market; business owners model revenue and expenses, buying behavior, and more; ecologists model population growth, rainfall, water levels, and soil composition, among many other things.
But, despite these many applications and the contributions it can make to general mathematical reasoning and critical thinking skills, mathematical modeling is rarely a main component of the math curriculum. Although textbook examples occasionally refer to real-world phenomena, the modeling process is not commonly practiced in the classroom.
Modeling involves engaging students in a big, messy real-world problem. The goals are for students to:
- refine their understanding of the situation by asking questions and making assumptions,
- leverage mathematical tools to solve the problem,
- make their own decisions about how to go about solving the problem,
- explain whether and how their methods and solutions make sense,
- and test or revise their solutions if necessary.
Mathematical modeling typically takes place over the course of several class sessions and involves working collaboratively with other students in small groups.
Modeling also offers the opportunity to integrate other material across the curriculum and to “think mathematically” in several different contexts. Modeling is not just about getting to a “right” answer — it’s about considering factors beyond mathematics as well. For example, students deal with questions like:
- What is a “fair” split?
- What level of risk should someone tolerate?
- What tradeoffs should a society make?
In others words, students come to see mathematics as the socially indispensable tool that it is, rather than an abstract (and sometimes frustrating) school subject.
Mathematical Modeling and Critical Thinking
Research suggests that the ability to solve abstractly framed academic math problems is not necessarily related to mathematical reasoning more broadly: that is, the ability to use math well in everyday life or to integrate mathematical thinking into one’s decision-making. Students may be able to follow procedures when given certain cues, but unable to reason about underlying concepts.
It’s also very common to hear complaints from students about math — that either they aren’t “math people,” that math is irrelevant, or that math is simply boring.
Mathematical modeling is one approach to resolving both these problems. It asks students to move between the concreteness of real — or at least relatively realistic — situations and the abstraction of mathematical models. Well-chosen problems can engage student interest. And the practice emphasizes revision, step-by-step improvement, and tradeoffs over single solution paths and single right-or-wrong answers.
Lesson Plan Outline
Mathematical modeling often begins with a general question, one that may initially seem only loosely related to mathematics:
- how to design an efficient elevator system, given certain constraints;
- what the best gas station is to visit in our local area;
- how to distinguish between two kinds of flies, given some data about their physical attributes.
Then, over the course of the modeling process, students develop more specific questions or cases, adding constraints or assumptions to simplify the problem. Along the way, students identify the important variables — what’s changing, and what’s not changing? Which variables are playing the biggest role in the desired outcomes?
Students with little experience in modeling can leap too quickly into looking for a generalized solution, before they have developed a feel for the problem. They may also need assistance in developing those specific cases. During this part of the process, it can be easiest to use well-defined values for some variables. These values may then become variables later on.
After students explore some simplifying cases, then they work on extensions of these cases to reach ever more general solutions.
Throughout the modeling process, the teacher may need to point out missing assumptions or constraints, or offer other ways of reframing the problem. For any given modeling problem, some solutions are usually more obvious than others, which leads to common stages students may reach as they solve the problem. But a key part of this activity is letting students be creative — students will often come up with unusual or especially innovative solutions.
A sample problem, from the Guidelines for Assessment and Instruction in Mathematical Modeling Education is below:
A
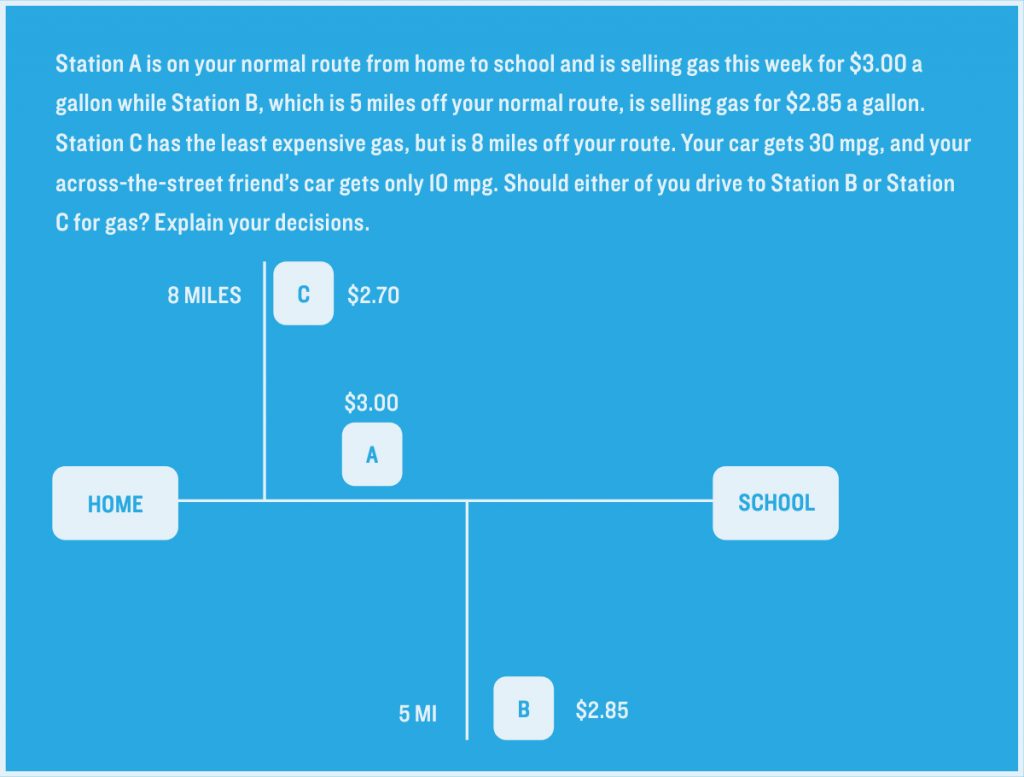
This problem involves variables that aren’t necessarily immediately apparent to students. For instance, the size of the gas tank, and how much gas you fill up on per trip. As students manage this specific case, they can take other hypothetical scenarios to generalize their solution: if it’s 10 miles away, how cheap would the gas have to be to make it worth it? What about the time spent in the car — is there a value to put on that?
Many modeling problems can be arbitrarily extended in various directions. Instead of just considering the best gas station to go to for a single car, for instance, students can explore the behavior of a fleet of trucks on set routes or seasonal changes to gas prices.
It’s also possible to include shorter modeling activities, where students work together in pairs or small groups to extend a problem or interpret the meaning of a solution.
These kinds of modeling activities are not reserved solely for older students. One example of a modeling problem for students in elementary school might be something like: what should go in a lunchbox? Students can talk about what kinds of things are important to them for lunch, “mathematize” the problem by counting student preferences or coming up with an equation (e.g., lunch = sandwich + vegetable + dessert + drink); and even explore geometrically how to fit such items into a lunchbox of a certain size.
Teaching Mathematical Modeling: Further Key Factors
Mathematical modeling activities can be challenging for both teachers and students.
Often, mathematical modeling activities stretch over several class periods. Fitting modeling activities in, especially if standardized tests are focused on mathematical content, can be challenging. One approach is to design modeling activities that support the overall content goals.
The teacher’s role during mathematical modeling is more like a facilitator than a lecturer. Mathematical modeling activities are considerably more open-ended than typical math activities, and require active organization, monitoring, and regrouping by the teacher. Deciding when to let students persevere on a problem for a bit longer and when to stop the class to provide additional guidance is a key skill that only comes with practice.
Students — especially students who have traditionally been successful in previous math classes — may also experience frustration when encountering modeling activities for the first time. Traditional math problems involve applying the right procedure to a well-defined problem. But expertise at this kind of mathematical reasoning differs markedly from tackling yet-to-be-defined problems with many possible solutions, each of which has tradeoffs and assumptions. Students might feel unprepared or even that they’re being treated unfairly.
Students also have to have some knowledge about the situation to reason mathematically about it. If the question is about elevators, for example, they need to know that elevators in tall buildings might go to different sets of floors; that elevators have a maximum capacity; that elevators occasionally break and need to be repaired.
Finally, the mathematical question needs to be tailored to students’ experience and interests. Asking a group of students who don’t drive about how to efficiently purchase gas won’t garner student interest. Teachers should use their familiarity with their students to find and design compelling modeling projects. This is chance for both students and teachers to be creative.
Sources and Resources
O’Connell, S. (2000).Introduction to Problem Solving: Strategies for The Elementary Classroom. Heinemann.
A recent handbook for teachers with tips on how to implement small-group problem solving.
Youcubed.org, managed by Jo Boaler.
A community with lots of resources for small-group problem solving instruction.
Yackel, E., Cobb, P., & Wood, T. (1991). Small group interactions as a source of learning opportunities in second-grade mathematics. Journal for research in mathematics education, 390-408.
Education research that illustrates how small-group problem solving leads to different kinds of learning opportunities than traditional instruction.
Guidelines for Assessment and Instruction in Mathematical Modeling Education, 2nd ed. (2019). Consortium for Mathematics and its Applications & Society for Industrial and Applied Mathematics.
An extensive guide for teaching mathematical modeling at all grade levels.
Hernández, M. L., Levy, R., Felton-Koestler, M. D., & Zbiek, R. M. (March/April 2017). Mathematical modeling in the high school curriculum. The variable, 2(2).
A discussion of the advantages of mathematical modeling at the high school level.
Corrêa, P. M. D. (2017). Observing high-school students’ mathematical understanding and mathematical proficiency in the context of mathematical modeling (Dissertation). University of Alberta, Alberta, Canada.
A dissertation exploring the various educational advantages of mathematical modeling.
